Research interests
My overall goal is to advance the research of computational and learning algorithms, using principles in applied mathematics and physics, to change the world for the better. In general, I am interested in optimization, machine learning, dynamical systems, and control theory.
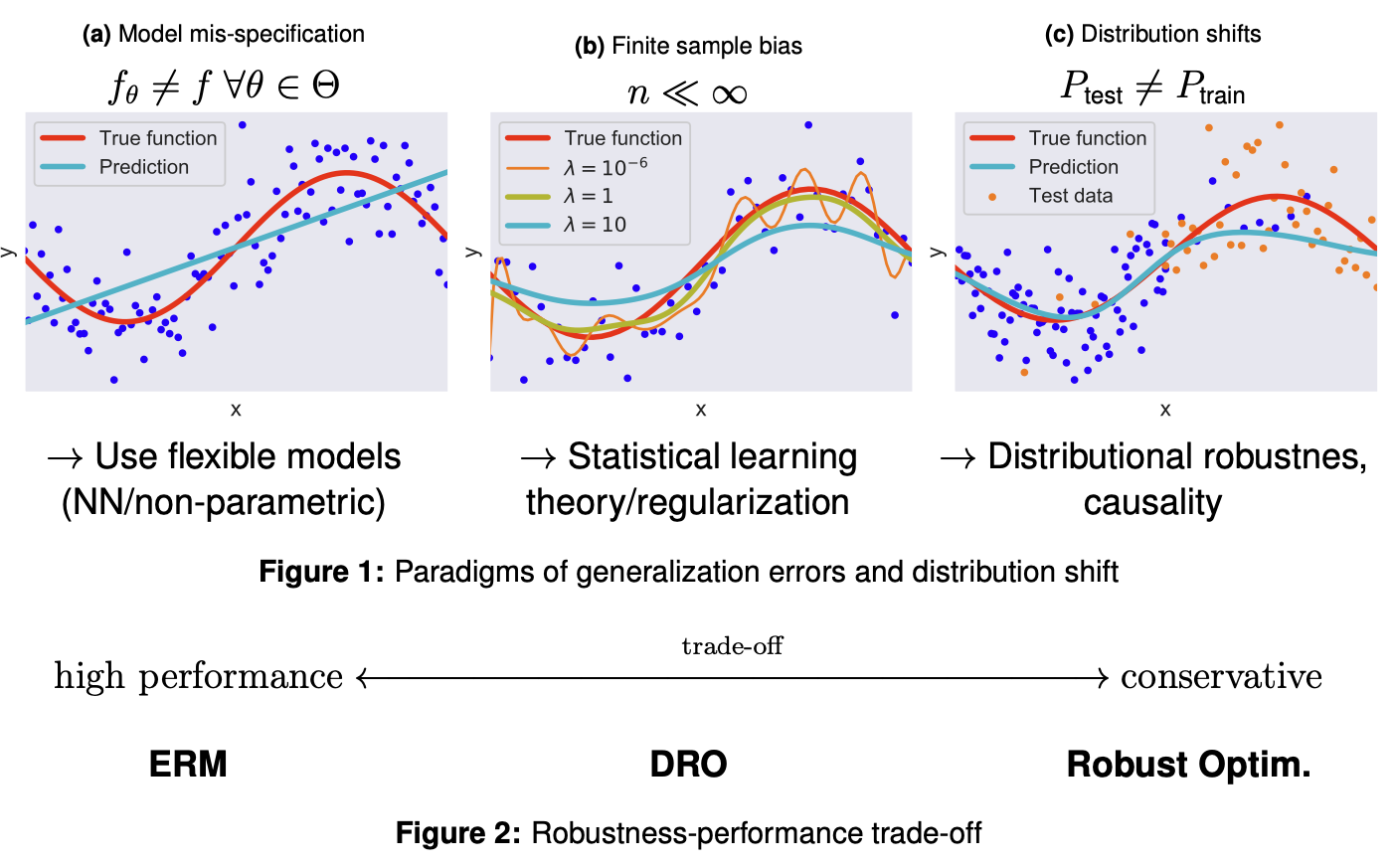
On one hand, I am motivated by addressing the lack of robustness and data distribution shift issues in modern learning algorithms. This lack of robustness can be the consequence of biases or unfairness in training data, adversarial attacks, offline data in RL, or causal confounding. For example, I have worked on the theory and computation algorithm to robustly learn ML models by optimizing the risk
\[\min_\theta \sup _ {P\in \mathcal M}\mathbb E_{X,Y\sim P} l(f_\theta(X), Y),\]where the underlying data distribution \(P\) is not the typical empirical average distribution used in statistical learning risk minimization \(\min_\theta \frac1N\sum_{i=1}^N l(\theta, \xi_i)\), but selected from an ambiguity set \(\mathcal M\) to endow robustness to the learning model.
On the other hand, I am interested in interfacing dynamical systems and machine learning (e.g., gradient flow, PDE theory for optimal transport, feedback control theory, robustness of deep learning models, and generative models), aiming at building robust and scalable optimization and learning algorithms. The dynamics perspective of ML and optimization is distinct from a static one in that it views quantities as time-evolutionary processes. For example, the aforementioned data distribution can be described by an evolutionary differential equation (PDE or SDE)
\[\partial _t \mu_t(x) = \mathcal L(\mu_t(x)),\]where just as in continuous optimization, the differential equation can be driven by the gradient of certain system energy encoded in the operator \(\mathcal L\). Our goal is then to study this time evolution of the data distribution \(\mu_t(x)\) for large-scale computation and learning. Different from, for example, classical PDE methods, we take a variational approach to dynamical systems, i.e., we view the time-evolution to be driven by an energy functional \(\mathcal E\). This is equivalent to viewing the dynamics as the solution to an optimization problem
\[\min_\mu \mathcal{E}(\mu).\]All those research topics call for a new generation of computational algorithms that can manipulate probability distributions and large-scale data structures robustly. Some example technical topics include
- machine learning applications of optimal transport and kernel methods; generative models
- robust machine learning, learning under distribution shift
- distributionally robust optimization, optimization under uncertainty
- numerical optimization, numerical methods
- control, dynamical systems, multi-stage decision-making
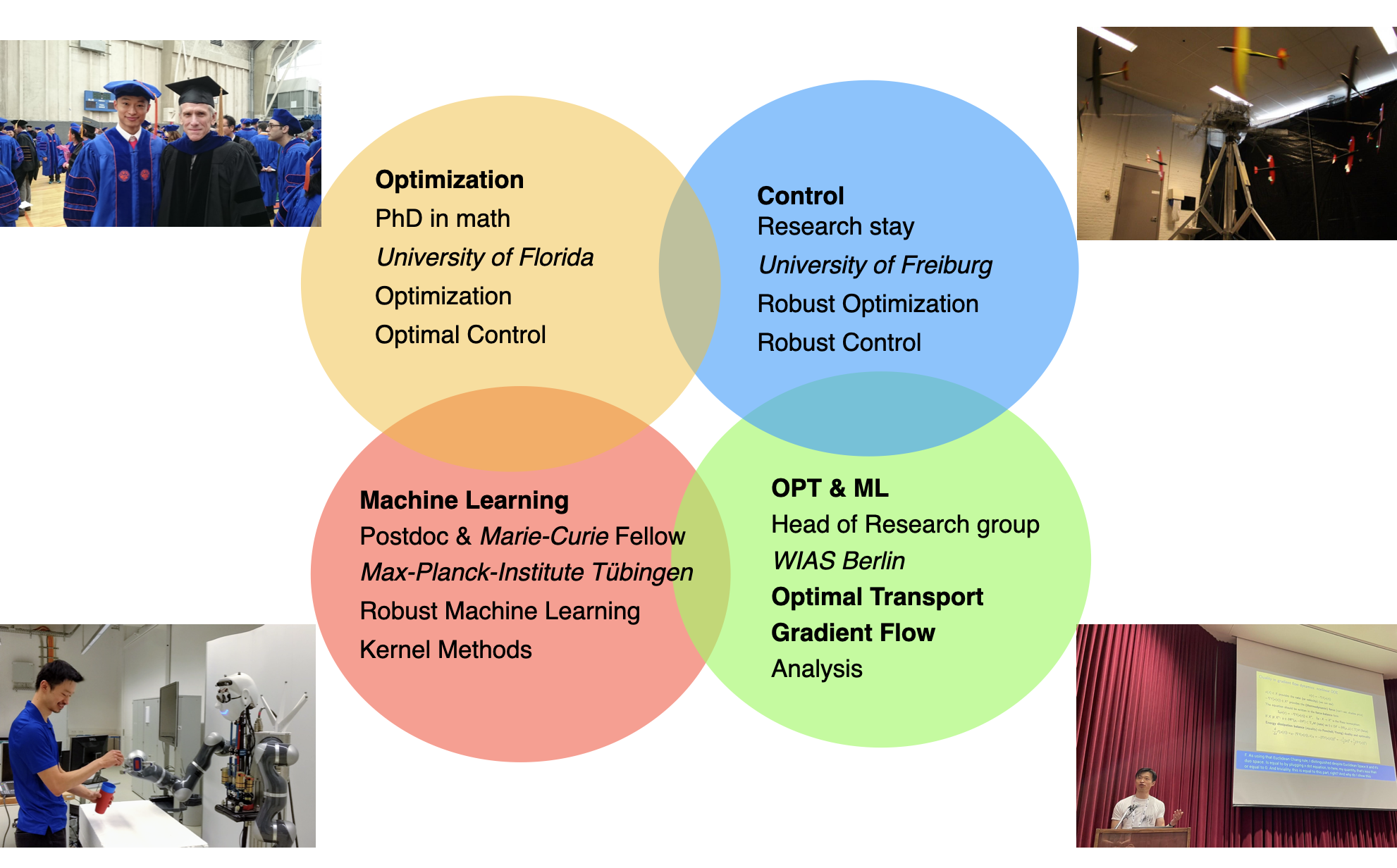
Below is a high-level illustration of my research journey
Publications, preprints, code
Approximation, Kernelization, and Entropy-Dissipation of Gradient Flows: from Wasserstein to Fisher-Rao. Jia-Jie Zhu, Alexander Mielke. preprint.
An Inexact Halpern Iteration with Application to Distributionally Robust Optimization. Ling Liang, Kim-Chuan Toh, Jia-Jie Zhu. preprint
Analysis of Kernel Mirror Prox for Measure Optimization. Pavel Dvurechensky, Jia-Jie Zhu. AISTATS 2024 (accepted) preprint
Estimation Beyond Data Reweighting: Kernel Method of Moments. Heiner Kremer, Yassine Nemmour, Bernhard Sch ̈olkopf, and Jia-Jie Zhu. In (to appear) Proceedings of the 40th International Conference on Machine Learning, Proceedings of Machine Learning Research. PMLR, 2023. paper code
Propagating Kernel Ambiguity Sets in Nonlinear Data-driven Dynamics Models. Jia-Jie Zhu. Accepted in the 62nd IEEE Conference on Decision and Control (CDC). preprint
Wasserstein Distributionally Robust Nonlinear Model Predictive Control. Zhengang Zhong, Jia-Jie Zhu. preprint
Functional Generalized Empirical Likelihood Estimation for Conditional Moment Restrictions. Heiner Kremer, Jia-Jie Zhu, Krikamol Muandet, and Bernard Schölkopf. In the Proceedings of the 39th International Conference on Machine Learning (ICML). PMLR, 2022. paper poster
Maximum Mean Discrepancy Distributionally Robust Nonlinear Chance-Constrained Optimization with Finite-Sample Guarantee Yassine Nemmour, Heiner Kremer, Bernhard Schölkopf, Jia-Jie Zhu. To appear in the 61st IEEE Conference on Decision and Control (CDC). preprint code (summer school exercises) slides (summer school)
- Note: there is an issue with the proof in this paper: one should replace it with a uniform convergence bound.
Adversarially Robust Kernel Smoothing. Jia-Jie Zhu, Christina Kouridi, Yassine Nemmour, Bernhard Schölkopf. Proceedings of The 25th International Conference on Artificial Intelligence and Statistics, volume 151 of Proceedings of Machine Learning Research, pages 4972–4994. PMLR, 28–30 Mar 2022. paper code slides (oral) poster
Learning Random Feature Dynamics for Uncertainty Quantification. Diego Agudelo-Espana, Yassine Nemmour, Bernhard Schölkopf, Jia-Jie Zhu. To appear in the 61st IEEE Conference on Decision and Control (CDC). preprint
Distributionally Robust Trajectory Optimization Under Uncertain Dynamics via Relative-Entropy Trust Regions. Hany Abdulsamad, Tim Dorau, Boris Belousov, Jia-Jie Zhu and Jan Peters. preprint
Distributional Robustness Regularized Scenario Optimization with Application to Model Predictive Control. Yassine Nemmour, Bernhard Schölkopf, Jia-Jie Zhu, 2021. Proceedings of the Conference on Learning for Dynamics and Control (L4DC). paper
Kernel Distributionally Robust Optimization. Jia-Jie Zhu, Wittawat Jitkrittum, Moritz Diehl, Bernhard Schölkopf, 2020. The conference version of this paper appeared in the Proceedings of the 24th International Conference on Artificial Intelligence and Statistics (AISTATS) 2021, San Diego, California, USA. PMLR: Volume 130. paper code slides (shorter version) (longer version)
Worst-Case Risk Quantification under Distributional Ambiguity using Kernel Mean Embedding in Moment Problem. Jia-Jie Zhu, Wittawat Jitkrittum, Moritz Diehl, Bernhard Schölkopf, 2020. In the 59th IEEE Conference on Decision and Control (CDC)), 2020. paper slides
Projection Algorithms for Non-Convex Minimization with Application to Sparse Principal Component Analysis. J.J. Zhu, D. Phan, W. Hager, 2015. Journal of Global Optimization, 65(4):657–676, 2016. paper code
A Kernel Mean Embedding Approach to Reducing Conservativeness in Stochastic Programming and Control. Zhu, Jia-Jie, Moritz Diehl and Bernhard Schölkopf. 2nd Annual Conference on Learning for Dynamics and Control (L4DC). In Proceedings of Machine Learning Research vol 120:1–9, 2020. paper slides
A New Distribution-Free Concept for Representing, Comparing, and Propagating Uncertainty in Dynamical Systems with Kernel Probabilistic Programming. Zhu, Jia-Jie, Krikamol Muandet, Moritz Diehl, and Bernhard Schölkopf. 21st IFAC World Congress. In IFAC-PapersOnLine proceedings, 2020. paper slides
Fast Non-Parametric Learning to Accelerate Mixed-Integer Programming for Online Hybrid Model Predictive Control. Zhu, Jia-Jie, and Martius, Georg. 21st IFAC World Congress. In IFAC-PapersOnLine proceedings, 2020. paper slides
Robust Humanoid Locomotion Using Trajectory Optimization and Sample-Efficient Learning. Yeganegi, Mohammad Hasan, Majid Khadiv, S Ali A Moosavian, Jia-Jie Zhu, Andrea Del Prete, and Ludovic Righetti. IEEE Humanoids, 2019. paper
Generative Adversarial Active Learning. J.J. Zhu, J. Bento, 2017. NIPS 2017 Workshop on Teaching Machines, Robots, and Humans. paper
Control What You Can: Intrinsically Motivated Task-Planning Agent. Blaes, Sebastian, Marin Vlastelica Pogančić, JJ Zhu, and Georg Martius. In Advances in Neural Information Processing Systems (NeurIPS) 32, pages 12541– 12552. Curran Associates, Inc., 2019. paper
Deep Reinforcement Learning for Resource-Aware Control. D. Baumann, J.J. Zhu, G. Martius, S. Trimpe, 2018. IEEE CDC 2018. paper code
A Metric for Sets of Trajectories that is Practical and Mathematically Consistent. J. Bento, J.J. Zhu, 2016. paper
A Decentralized Multi-Block Algorithm for Demand-Side Primary Frequency Control Using Local Frequency Measurements. J. Brooks, W. Hager, J.J. Zhu, 2015. paper
Previous projects
- Kernel machine learning for distributionally robust optimization, Empirical Inference Department, Max Planck Institute for Intelligent Systems, Tübingen
- Marie Skołodowska-Curie Individual Fellowship on learning-control algorithms, Max Planck Institute for Intelligent Systems, Tübingen
- (More under construction …)
Open-source code
See above for more code associated with publications.
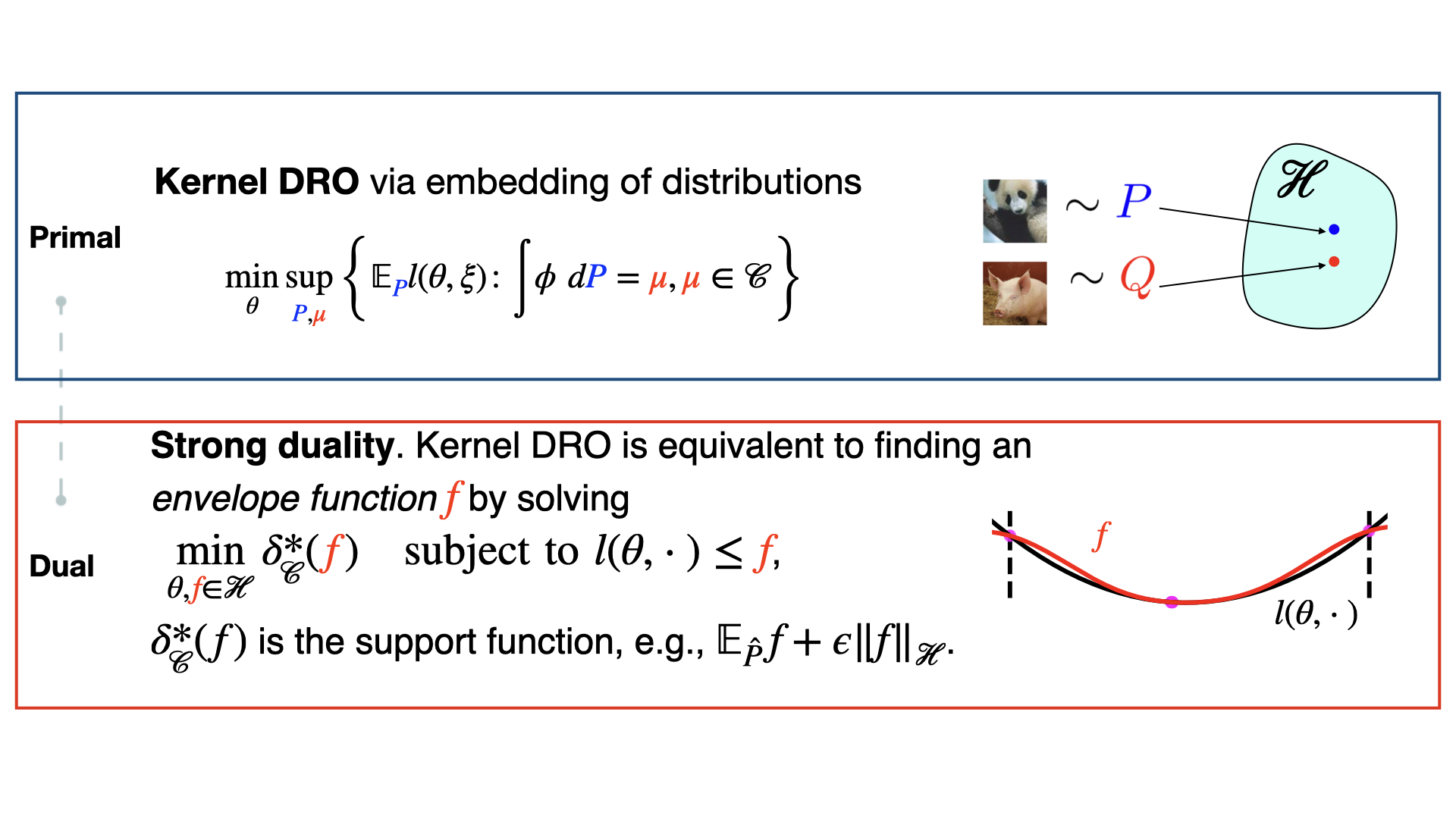
K-DRO – Kernel Distributionally Robust Optimization
K-DRO is the software implementation of Kernel Distributionally Robust Optimization (DRO), a robust machine learning and optimization algorithm that can handle nonlinear non-convex loss and model functions. It is based on a dual reformulation that turns an DRO problem into a kernel learning problem. The intuition is to find a smooth kernel function that majorizes the original loss, as demonstrated in the illustration below.
More information: https://github.com/jj-zhu/kdro
K-MoM - Kernel Method of Moments
This software repository contains several state-of-the-art estimation tools for (conditional) moment restriction problems, e.g., for instrumental variable (IV) regression.
More information: https://github.com/HeinerKremer/conditional-moment-restrictions
MMD-DR-CCSP – Maximum Mean Discrepancy Distributionally Robust Nonlinear Chance-Constrained Programming
MMD-DR-CCSP applies the Kernel Distributionally Robust Optimization methodology. Compared with other DR-CCSP algorithms, it can handle nonlinear change constraints with computable finite-sample guarantees.
More information: https://github.com/yasnem/CC_Tutorial_TUB_Oxford
ARKS – Adversarially Robust Kernel Smoothing
ARKS is a large-scale implementation of kernel methods for distributionally robust optimization. It is based on the idea of using a diffusion process to robustify the learning algorithms.
More information: https://github.com/christinakouridi/arks